Reconstruction and visualization

This is a brief tutorial that demonstrates how to do a basic reconstruction and visualization of a data set in 2D and 3D, and explains some of the parameters necessary for the reconstruction to work correctly. The reconstruction only requires the usage of CPU resources. The simulated data used in the rendered version of this tutorial can be obtained using, e.g., wget with

wget https://zenodo.org/records/7326784/files/saxstt_dataset_M.h5

[2]:

import h5py
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import display
# from ipywidgets import interact
from mumott.data_handling import DataContainer
from mumott.output_handling import ProjectionViewer
from mumott.output_handling.saving import dict_to_h5
from mumott.methods.basis_sets import SphericalHarmonics
from mumott.methods.projectors import SAXSProjector
from mumott.methods.residual_calculators import GradientResidualCalculator
from mumott.optimization.loss_functions import SquaredLoss
from mumott.optimization.optimizers import LBFGS
from mumott.optimization.regularizers import Laplacian

INFO:Setting the number of threads to 4. If your physical cores are fewer than this number, you may want to use numba.set_num_threads(n), and os.environ["OPENBLAS_NUM_THREADS"] = f"{n}" to set the number of threads to the number of physical cores n.
INFO:Setting numba log level to WARNING.

Loading data

First, we need to locate our input data. The path, name, and input type are defined as strings. The path can be either relative or absolute. The file name needs to include the file ending. The only allowed input format is 'h5' (which requires a specially formated hdf5 file).

Initializing the DataContainer

The input files must contain most of the necessary metadata, so creating a DataContainer object simply requires passing the file name as an argument.

[3]:

data_container = DataContainer('saxstt_dataset_M.h5')

INFO:Rotation matrix generated from inner and outer angles, along with inner and outer rotation axis vectors. Rotation and tilt angles assumed to be in radians.

/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/data_handling/data_container.py:227: DeprecationWarning: Entry name rotations is deprecated. Use inner_angle instead.
  _deprecated_key_warning('rotations')
/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/data_handling/data_container.py:236: DeprecationWarning: Entry name tilts is deprecated. Use outer_angle instead.
  _deprecated_key_warning('tilts')
/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/data_handling/data_container.py:268: DeprecationWarning: Entry name offset_j is deprecated. Use j_offset instead.
  _deprecated_key_warning('offset_j')
/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/data_handling/data_container.py:278: DeprecationWarning: Entry name offset_k is deprecated. Use k_offset instead.
  _deprecated_key_warning('offset_k')

INFO:No sample geometry information was found. Default mumott geometry assumed.
INFO:No detector geometry information was found. Default mumott geometry assumed.

We can now take a quick look at the container object to see that the parameters make sense.

[4]:

display(data_container)

DataContainer

Field	Size
Number of projections	417
Corrected for transmission	False

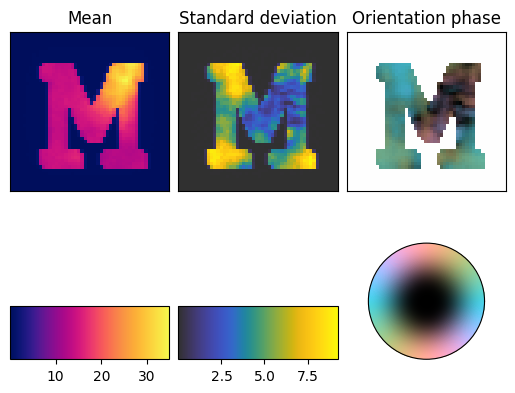
We can use the ProjectionViewer to check out projections. For interactive usage, it would be necessary to use the setting %matplotlib widget, but for the purpose of correctly rendering the widget in HMTL, this is left out.

[6]:

p = ProjectionViewer(data_container, orientation_symmetry='transversal')

/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/output_handling/orientation_image_mapper.py:22: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  self._colormap = get_cmap(colormap)
/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/output_handling/projection_viewer.py:137: MatplotlibDeprecationWarning: The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.
  self._phase_colormap_lut = cm.get_cmap(self._phase_colormap, 256)
/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/colorspacious/ciecam02.py:333: RuntimeWarning: invalid value encountered in divide
  t = (C

../_images/tutorials_reconstruct_and_visualize_8_1.png

We now need to choose a basis set (we choose SphericalHarmonics with ell_max=6), a projector (we use SAXSProjector, which is slow but runs on a CPU), a ResidualCalculator (we use GradientResidualCalculator), a loss function (we use a standard SquaredLoss), and an optimizer (we use LBFGS).

We also add a regularizer (the Laplacian) and append it to the loss function with a weight of 1e-2.

[7]:

basis_set = SphericalHarmonics(ell_max=6)
display(basis_set)

/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/methods/basis_sets/spherical_harmonics.py:105: DeprecationWarning: `scipy.special.sph_harm` is deprecated as of SciPy 1.15.0 and will be removed in SciPy 1.17.0. Please use `scipy.special.sph_harm_y` instead.
  complex_factors = sph_harm(abs(self._emm_indices)[np.newaxis, np.newaxis, np.newaxis, ...],

SphericalHarmonics

Field	Size	Data
Maximum "ell"	1	6
"ell" indices	28	[0 2 ... 6 6]
"emm" indices	28	[ 0 -2 ... 5 6]
Coefficient projection matrix	(1, 1, 28)	[[[1.00e+00 0.00e+00 ... 5.14e-16 2.42e+00]]]
Hash	17	19d40d

[8]:

projector = SAXSProjector(data_container.geometry)
display(projector)

SAXSProjector

Field	Size	Data
is_dirty	1	False
hash	17	abf2e6

[14]:

residual_calculator = GradientResidualCalculator(
                                data_container=data_container,
                                basis_set=basis_set,
                                projector=projector)
display(residual_calculator)

GradientResidualCalculator

Field	Size	Data
BasisSet	1	SphericalHarmonics
Projector	13	SAXSProjector
Is dirty	1	False
probed_coordinates	(417, 8, 3, 3)	0x5c17 (hash)
Hash	18	101e80

[15]:

loss_function = SquaredLoss(residual_calculator)
display(loss_function)

LossFunction

Field	Size	Data
ResidualCalculator	1	GradientResidualCalculator
use_weights	1	False
preconditioner_hash	1	None
residual_norm_multiplier	1	1
Function of residual r	1	$L(r) = r^2$
Use preconditioner mask	1	True
Hash	17	df43e7

[16]:

regularizer = Laplacian()
loss_function.add_regularizer(name='laplacian',
                              regularizer=regularizer,
                              regularization_weight=1e-1)
display(regularizer)

Laplacian

Field	Size	Data
Function of coefficients	1	$R(\vec{x}) = \lambda \frac{\Vert \nabla^2 \vec{x} \Vert^2}{2}$
Hash	18	1df556

[17]:

optimizer = LBFGS(loss_function, maxiter=10)
display(optimizer)

Optimizer

Field	Size	Data
LossFunction	1	SquaredLoss
Hash	17	fc79d6
options[maxiter]	1	10

To suppress excessive output from running the optimization, we will get the 'mumott.optimization.optimizer' logger and set the level to logging.WARNING, which will suppress INFO outputs.

[18]:

results = optimizer.optimize()

  0%|          | 0/10 [00:00<?, ?it/s]

/das/home/carlse_m/p20850/envs/mumott_latest/lib/python3.11/site-packages/mumott/optimization/optimizers/lbfgs.py:121: DeprecationWarning: scipy.optimize: The `disp` and `iprint` options of the L-BFGS-B solver are deprecated and will be removed in SciPy 1.18.0.
  result = minimize(fun=loss_function_wrapper, callback=progress_callback,

100%|██████████| 10/10 [02:00<00:00, 12.07s/it]

We use the basis_set to get a number of tensor-quantities out of the optimized coefficients:

output.mean_intensity is the mean scattering power, averaged over all directions.
output.fractional anisotropy is a measure of how anisotropic the scattering is each voxel.
output.second_moment_tensor is a rank-2 tensor (3-by-3 matrix) that contains information about both the intensity, anisotropy and orientation of the scattering.
output.eigenvalue_1 is the smallest eigenvalue of the second moment tensor. output.eigenvalue_3 is the largest eigenvalue.
output.eigenvector_1 is the corresponding egenvector. In samples that have apoproximate axial symmetry on the voxel length scale, either output.eigenvector_1 or output.eigenvector_3 provide an estimate of the symmetry axis, depending on the formfactor. For equatorial ring type scattering output.eigenvector_1 is apropriate. For polar cap type scattering, output.eigenvector_3.

[19]:

output = basis_set.get_output(residual_calculator.coefficients)

Visualizing the output

We want to take a look at the orientations of our sample, the output contains the quantities, output.mean_intensity, output.fractional_anisotropy and output.eigenvector_3 for scale, color and orientation vector respectively. The third eigenvector corresponds to the largest eigenvalue, i.e. the direction with the strongest scattering.

[24]:

orientation = output.eigenvector_3
scale = output.mean_intensity
color = output.fractional_anisotropy

To do a 3D render, we use mayavi, a VTK frontend. This is a convenient package for viewing 3D data in Python, but not mandatory, as there are many other alternatives. For notebook rendering, we will use the png backend to make the render persist in the notebook; for interactive plots, ipy is preferable.

[25]:

import colorcet
from matplotlib import colormaps as cm

[26]:

orientation.shape

[26]:

(50, 50, 50, 3)

We want to threshold the scale and color, so we will plot a slice of each.

[28]:

f, ax = plt.subplots(2, figsize=(5, 9))
image_0 = ax[0].imshow(scale[:, 25, :], cmap='cet_gouldian')
plt.colorbar(image_0, ax=ax[0])
image_1 = ax[1].imshow(color[:, 25, :], cmap='cet_fire')
plt.colorbar(image_1, ax=ax[1])
display(image_0)
display(image_1)

<matplotlib.image.AxesImage at 0x14723b07e650>

<matplotlib.image.AxesImage at 0x14723b234890>

../_images/tutorials_reconstruct_and_visualize_26_2.png

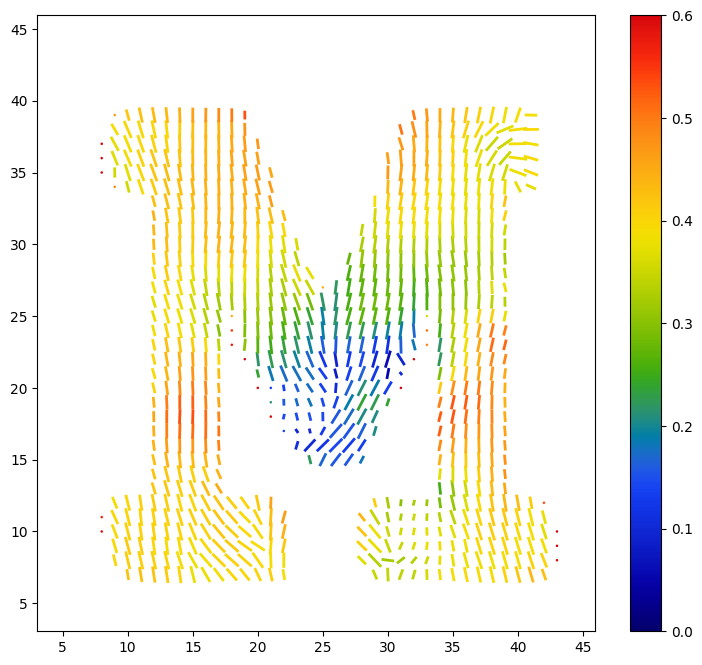
Based on these images, we will choose 0.4 and 1.0 as our cutoffs for the scale, and 0.0 and 0.6 as our cutoffs for the color. We check our reconstruction out using matplotlib.pyplot.quiver, which can also be a useful alternative to 3D rendering.

[38]:

scale_cutoff = (0.3, 1.0)
color_cutoff = (0.0, 0.6)
test_scale = scale[5:45, 25, 5:45].clip(0, scale_cutoff[1])
test_scale[test_scale < scale_cutoff[0]] = np.nan
test_scale -= scale_cutoff[0]
test_scale /= (scale_cutoff[1] - scale_cutoff[0])
test_color = color[5:45, 25, 5:45].clip(*color_cutoff)
f, ax = plt.subplots(1, figsize=(9, 8))
x, y = np.meshgrid(np.arange(5, 45),
                   np.arange(5, 45),
                   indexing='ij')
test_orientation_x = orientation[5:45, 25, 5:45, 0] * test_scale
test_orientation_y = orientation[5:45, 25, 5:45, 2] * test_scale * np.sign(test_orientation_x)
test_orientation_x = abs(test_orientation_x)
q = ax.quiver(x, y, test_orientation_x, test_orientation_y,
              test_color, pivot='mid', angles='xy',
              headwidth=1, headlength=0, scale=30, width=0.005,
              cmap='cet_rainbow4', clim=color_cutoff)
plt.colorbar(q, ax=ax)
display(q)

<matplotlib.quiver.Quiver at 0x147233f710d0>

../_images/tutorials_reconstruct_and_visualize_28_1.png

This concludes the tutorial.