Regularization L-curves¶
This tutorial demonstrates how to do a regularization L-curve, using the Spherical Integral Geometric Tensor Tomography (SIGTT) pipeline as a guiding example, since it has a built-in regularizer.
The dataset of trabecular bone used in this tutorial is available via Zenodo, and can be downloaded either via a browser or the command line using, e.g., wget or curl,
wget https://zenodo.org/records/10074598/files/trabecular_bone_9.h5
[1]:
import warnings
from mumott.data_handling import DataContainer
from mumott.pipelines import run_sigtt
import matplotlib.pyplot as plt
import colorcet
import logging
import numpy as np
data_container = DataContainer('trabecular_bone_9.h5')
INFO:Setting the number of threads to 8. If your physical cores are fewer than this number, you may want to use numba.set_num_threads(n), and os.environ["OPENBLAS_NUM_THREADS"] = f"{n}" to set the number of threads to the number of physical cores n.
INFO:Setting numba log level to WARNING.
INFO:Inner axis found in dataset base directory. This will override the default.
INFO:Outer axis found in dataset base directory. This will override the default.
INFO:Rotation matrices were loaded from the input file.
INFO:Sample geometry loaded from file.
INFO:Detector geometry loaded from file.
SIGTT - Spherical Integral Geometric Tensor Tomgraphy¶
SIGTT is a relatively straightforward reconstruction method. The reciprocal space map at one q-bin is a function on the sphere, and therefore it can be expressed in spherical harmonics. They are orthogonal and rotationally invariant, and therefore converge easily. Correlation between neighbours can be easily expressed in terms of the spherical harmonic inner product, or power-spectrum function, and one can maximize this correlation by minimizing the Laplacian. This is the basic motivation behind the SIGTT pipeline.
The pipeline uses the LBFGS-B optimizer. We will first run the pipeline without any regularization by setting the weight to zero. We will use an ftol of 1e-4, maxiter of 50, and maxfun of np.inf, to discourage overly eager convergence.
[2]:
%%time
result = run_sigtt(data_container,
use_gpu=True,
optimizer_kwargs=dict(ftol=1e-4, maxfun=np.inf, maxiter=50),
regularization_weight=0.)
reconstruction = result['result']['x']
basis_set = result['basis_set']
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 46/50 [01:48<00:09, 2.37s/it]
CPU times: user 3min 57s, sys: 11min 46s, total: 15min 43s
Wall time: 1min 48s
To analyze the results we here define a convenience function that allows us to extract mean, standard deviation, and orientation data from the reconstruction.
[3]:
def get_tensor_properties(basis_set, reconstruction):
with warnings.catch_warnings():
warnings.filterwarnings('ignore', r'invalid value encountered in divide')
spherical_functions = basis_set.get_output(reconstruction[28:29])['spherical_functions']
mean = spherical_functions['means'][0, ...]
std = np.sqrt(spherical_functions['variances'][0, ...])
eigenvectors = spherical_functions['eigenvectors']
orientation = np.arctan2(-eigenvectors[0, ..., 1, 0],
eigenvectors[0, ..., 2, 0])
orientation[orientation < 0] += np.pi
orientation[orientation > np.pi] -= np.pi
orientation *= 180 / np.pi
orientation_alpha = np.clip(2 * std / std.max(), 0, 1)
return mean, std, orientation, orientation_alpha
[4]:
mean, std, orientation, orientation_alpha = get_tensor_properties(basis_set, reconstruction)
Next we plot the results.
[5]:
colorbar_kwargs = dict(orientation='horizontal', shrink=0.75, pad=0.1)
mean_kwargs = dict(vmin=0, vmax=800, cmap='cet_gouldian')
std_kwargs = dict(vmin=0, vmax=400, cmap='cet_fire')
orientation_kwargs = dict(vmin=0, vmax=180, cmap='cet_CET_C10')
def config_cbar(cbar):
cbar.set_ticks([i for i in np.linspace(0, 180, 5)])
cbar.set_ticklabels([r'$' + f'{int(v):d}' + r'^{\circ}$' for v in bar.get_ticks()])
[6]:
fig, ax = plt.subplots(1, 3, figsize=(10.3, 4.6), dpi=140, sharey=True)
im0 = ax[0].imshow(mean, **mean_kwargs);
im1 = ax[1].imshow(std, **std_kwargs);
im2 = ax[2].imshow(orientation, alpha=orientation_alpha, **orientation_kwargs);
ax[0].set_title('Mean amplitude')
ax[1].set_title('Anisotropic ampl.')
ax[2].set_title('Orientation')
plt.subplots_adjust(wspace=0)
plt.colorbar(im0, ax=ax[0], **colorbar_kwargs)
plt.colorbar(im1, ax=ax[1], **colorbar_kwargs)
bar = plt.colorbar(im2, ax=ax[2], **colorbar_kwargs)
config_cbar(bar)
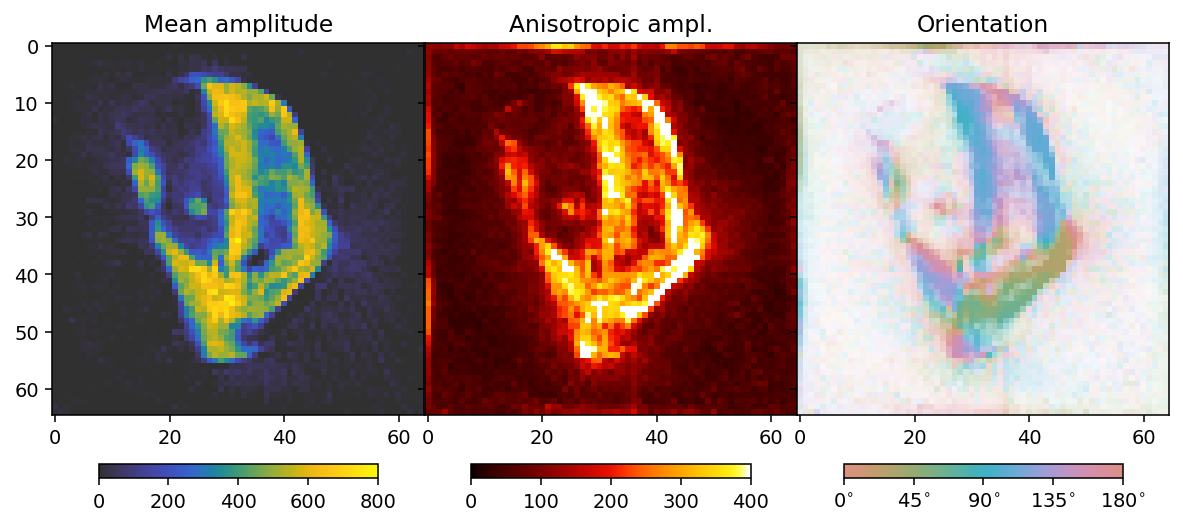
First regularization weight sweep¶
In order to find the optimal value for the regularization, we need to check a wide span, and investigate how the residual norm changes relative to the regularization norm.
[7]:
%%time
weights = np.geomspace(1e-2, 1e5, 5)
results = []
residual_norm = []
regularization_norm = []
for i, w in enumerate(weights):
results.append(run_sigtt(data_container,
use_gpu=True,
optimizer_kwargs=dict(ftol=1e-4, maxfun=np.inf, maxiter=50),
regularization_weight=w))
residual_norm.append(results[i]['loss_function'].get_residual_norm()['residual_norm'])
regularization_norm.append(results[i]['loss_function'].get_regularization_norm()['laplacian']['regularization_norm'])
94%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▎ | 47/50 [01:57<00:07, 2.50s/it]
92%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋ | 46/50 [01:14<00:06, 1.62s/it]
58%|██████████████████████████████████████████████████████████████████████████▊ | 29/50 [00:49<00:36, 1.72s/it]
60%|█████████████████████████████████████████████████████████████████████████████▍ | 30/50 [00:56<00:37, 1.89s/it]
32%|█████████████████████████████████████████▎ | 16/50 [00:42<01:29, 2.63s/it]
CPU times: user 13min 23s, sys: 39min 50s, total: 53min 14s
Wall time: 5min 41s
[8]:
reconstructions = [r['result']['x'] for r in results]
basis_sets = [r['basis_set'] for r in results]
[9]:
colorbar_kwargs = dict(orientation='horizontal', shrink=0.9, pad=0.03)
fig, axes = plt.subplots(ncols=3, nrows=5, figsize=(6.8, 12.8), dpi=140, sharey=True, sharex=True)
for i in range(5):
ax = axes[i]
mean, std, orientation, orientation_alpha = get_tensor_properties(basis_sets[i], reconstructions[i])
plt.subplots_adjust(wspace=0, hspace=0)
im0 = ax[0].imshow(mean, **mean_kwargs);
im1 = ax[1].imshow(std, **std_kwargs);
im2 = ax[2].imshow(orientation, alpha=orientation_alpha, **orientation_kwargs);
if i == 0:
ax[0].set_title('Mean amplitude')
ax[1].set_title('Anisotropic ampl.')
ax[2].set_title('Orientation')
ax[0].set_ylabel(r'$\lambda = ' + f'{weights[i]:.2e}' + r'$')
if i == 4:
plt.colorbar(im0, ax=axes[:, 0], **colorbar_kwargs);
plt.colorbar(im1, ax=axes[:, 1], **colorbar_kwargs);
bar = plt.colorbar(im2, ax=axes[:, 2], **colorbar_kwargs);
config_cbar(bar)
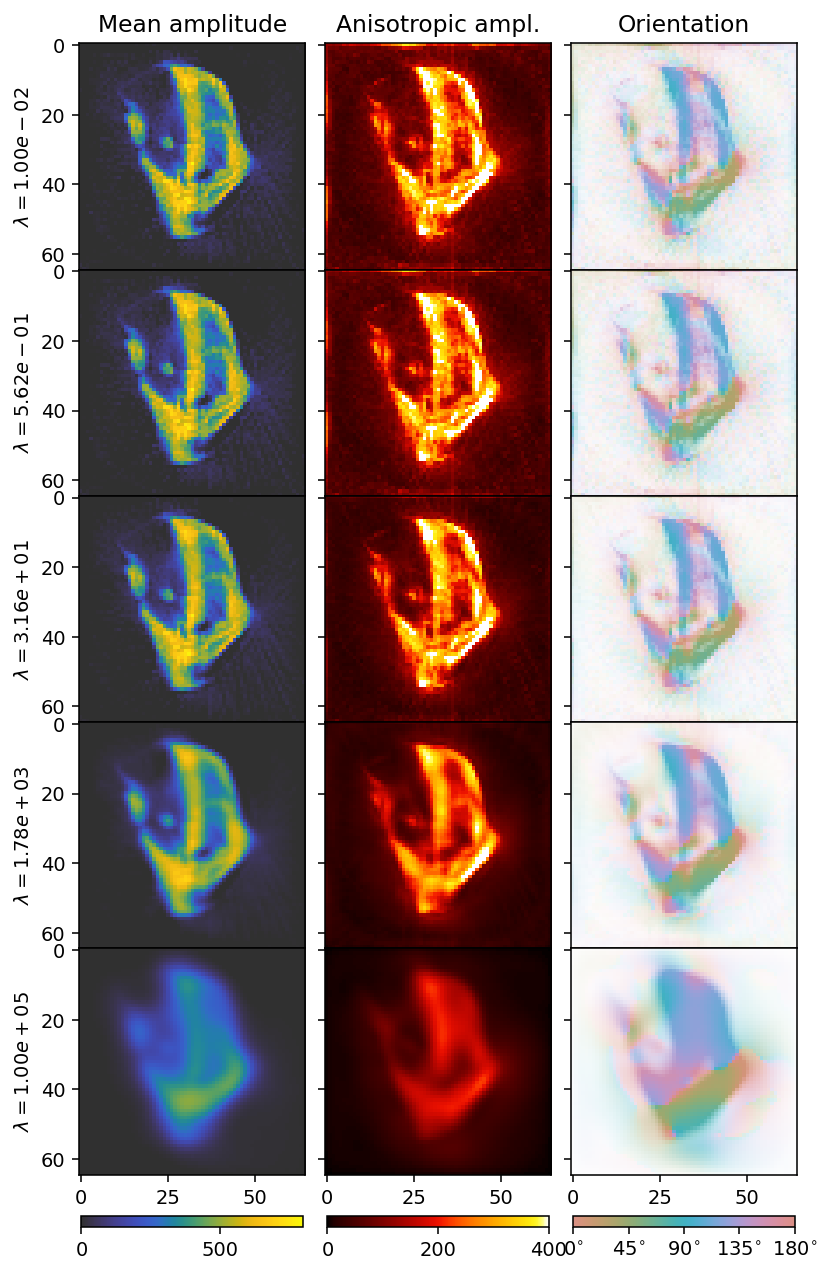
With increasing \(\lambda\), the reconstruction becomes blurrier. We can get a better idea by looking at the an L-curve.
[10]:
f, ax = plt.subplots(1, 1, figsize=(6, 3), dpi=140)
ax.loglog(residual_norm, regularization_norm, '--X')
for x, y, t in zip(residual_norm, regularization_norm, weights):
ax.text(x, y, f'{t:.2e}')
ax.set_ylabel('Laplacian L2 norm')
ax.set_xlabel('Residual norm')
[10]:
Text(0.5, 0, 'Residual norm')
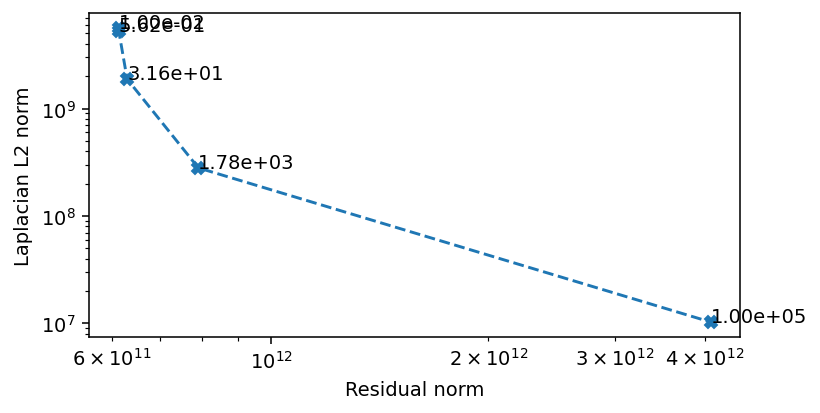
The critical area where the Laplacian L2 norm and the residual norm are simultaneously minimized is when the regularization weight is between \(1\) and \(1e4\). We scan this region in more detail to find a preferred value.
Second sweep¶
[11]:
%%time
weights = np.geomspace(1, 1e4, 5)
results = []
residual_norm = []
regularization_norm = []
for i, w in enumerate(weights):
results.append(run_sigtt(data_container,
use_gpu=True,
optimizer_kwargs=dict(ftol=1e-5, gtol=1e-7, maxfun=np.inf, maxiter=100),
regularization_weight=w))
residual_norm.append(results[i]['loss_function'].get_residual_norm()['residual_norm'])
regularization_norm.append(results[i]['loss_function'].get_regularization_norm()['laplacian']['regularization_norm'])
48%|█████████████████████████████████████████████████████████████▍ | 48/100 [01:19<01:26, 1.66s/it]
40%|███████████████████████████████████████████████████▏ | 40/100 [01:15<01:53, 1.89s/it]
24%|██████████████████████████████▋ | 24/100 [00:48<02:32, 2.01s/it]
17%|█████████████████████▊ | 17/100 [00:46<03:49, 2.76s/it]
28%|███████████████████████████████████▊ | 28/100 [00:51<02:11, 1.82s/it]
CPU times: user 13min 8s, sys: 36min 58s, total: 50min 7s
Wall time: 5min 2s
[12]:
reconstructions = [r['result']['x'] for r in results]
basis_sets = [r['basis_set'] for r in results]
[13]:
colorbar_kwargs = dict(orientation='horizontal', shrink=0.9, pad=0.03)
fig, axes = plt.subplots(ncols=3, nrows=5, figsize=(6.8, 12.8), dpi=140, sharey=True, sharex=True)
for i in range(5):
ax = axes[i]
mean, std, orientation, orientation_alpha = get_tensor_properties(basis_sets[i], reconstructions[i])
plt.subplots_adjust(wspace=0, hspace=0)
im0 = ax[0].imshow(mean, **mean_kwargs);
im1 = ax[1].imshow(std, **std_kwargs);
im2 = ax[2].imshow(orientation, alpha=orientation_alpha, **orientation_kwargs);
if i == 0:
ax[0].set_title('Mean amplitude')
ax[1].set_title('Anisotropic ampl.')
ax[2].set_title('Orientation')
ax[0].set_ylabel(r'$\lambda = ' + f'{weights[i]:.2e}' + r'$')
if i == 4:
plt.colorbar(im0, ax=axes[:, 0], **colorbar_kwargs);
plt.colorbar(im1, ax=axes[:, 1], **colorbar_kwargs);
bar = plt.colorbar(im2, ax=axes[:, 2], **colorbar_kwargs);
config_cbar(bar)
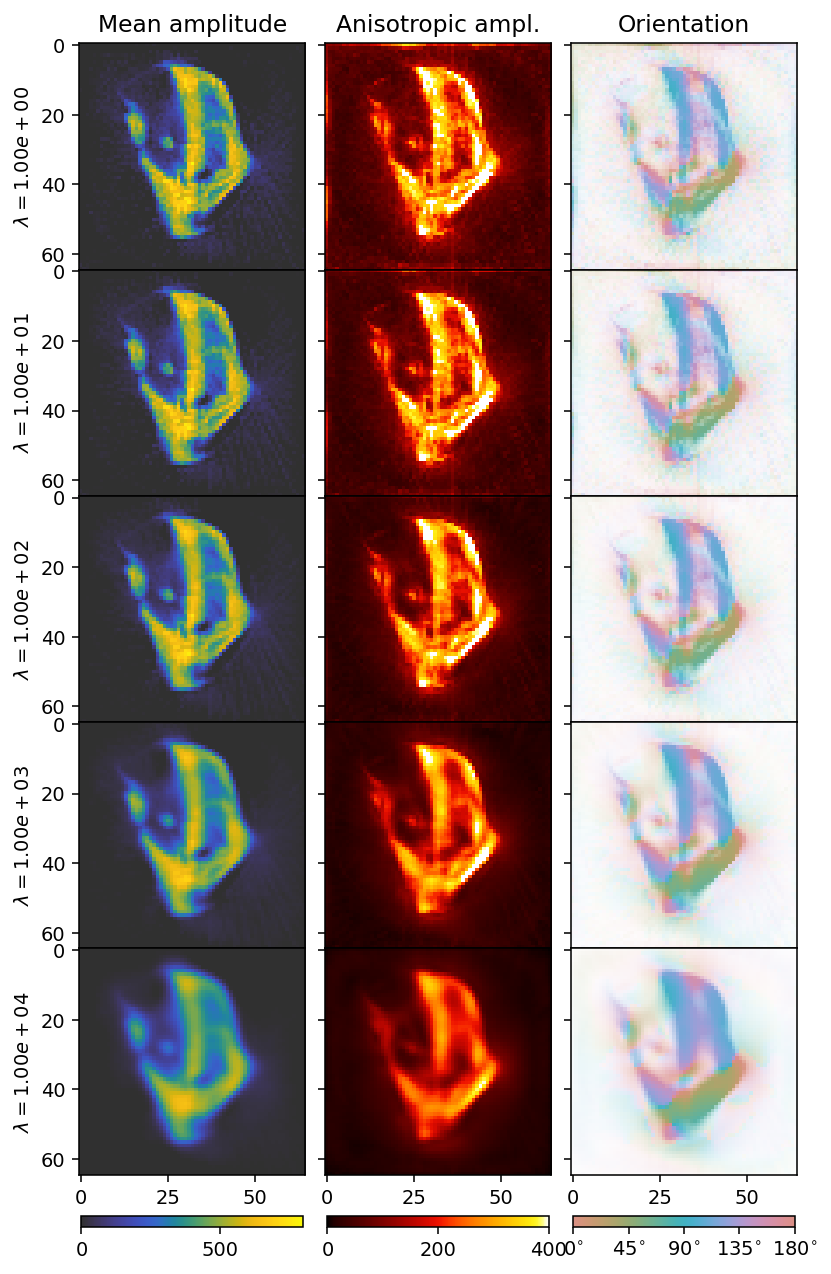
[14]:
f, ax = plt.subplots(1, 1, figsize=(6, 3), dpi=140)
ax.loglog(residual_norm, regularization_norm, '--X')
for x, y, t in zip(residual_norm, regularization_norm, weights):
ax.text(x, y, f'{t:.2e}')
ax.set_ylabel('Laplacian L2 norm')
ax.set_xlabel('Residual norm')
[14]:
Text(0.5, 0, 'Residual norm')
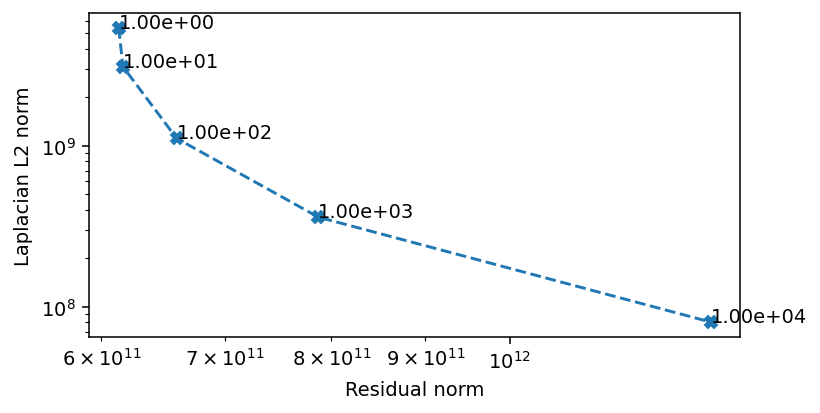
There seems to be three regions, which we can also infer from the convergence rate. At weights below \(1e1\) the convergence is dominated by the residual norm. Above \(1e3\) the convergence is dominated by the regularization. The area of interest ins the region in between, where we also see the most rapid convergence. We can conclude that a value in this range is likely to be optimal, and we opt for \(5e2\) as our weight.
The final result¶
[15]:
%%time
result = run_sigtt(data_container,
use_gpu=True,
optimizer_kwargs=dict(ftol=1e-5, gtol=1e-7, maxfun=np.inf, maxiter=100),
regularization_weight=5e2,
maxiter=100)
reconstruction = result['result']['x']
basis_set = result['basis_set']
17%|█████████████████████▊ | 17/100 [00:47<03:51, 2.79s/it]
CPU times: user 1min 51s, sys: 5min 41s, total: 7min 32s
Wall time: 47.5 s
[16]:
mean, std, orientation, orientation_alpha = get_tensor_properties(basis_set, reconstruction)
[17]:
fig, ax = plt.subplots(1, 3, figsize=(10.3, 4.6), dpi=140, sharey=True)
im0 = ax[0].imshow(mean, **mean_kwargs);
im1 = ax[1].imshow(std, **std_kwargs);
im2 = ax[2].imshow(orientation, alpha=orientation_alpha, **orientation_kwargs);
ax[0].set_title('Mean amplitude')
ax[1].set_title('Anisotropic ampl.')
ax[2].set_title('Orientation')
plt.subplots_adjust(wspace=0)
plt.colorbar(im0, ax=ax[0], **colorbar_kwargs)
plt.colorbar(im1, ax=ax[1], **colorbar_kwargs)
bar = plt.colorbar(im2, ax=ax[2], **colorbar_kwargs)
config_cbar(bar)
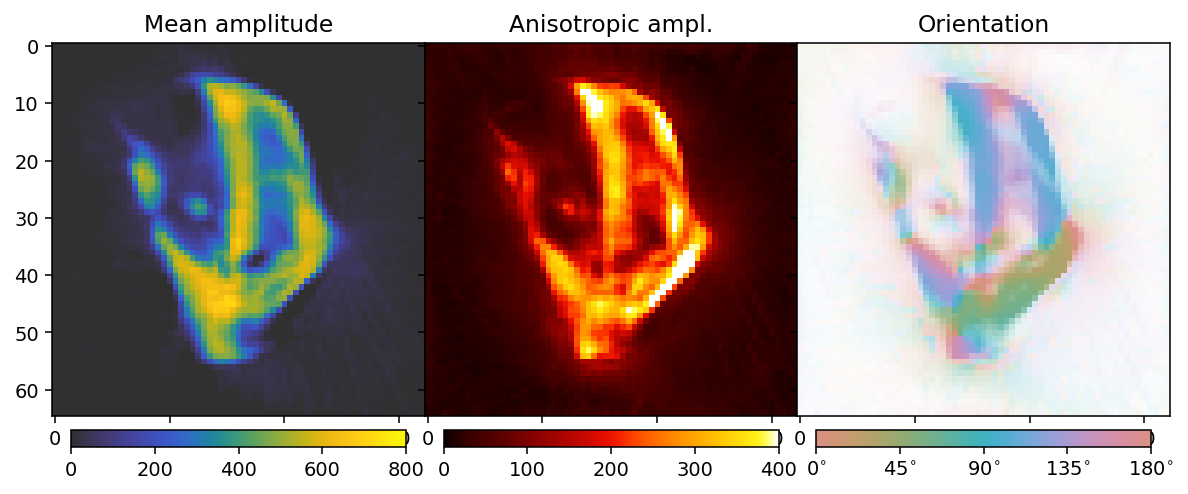
This reconstruction has a reasonable tradeoff between blurring detail and reducing noise. The Laplacian has drawbacks as a regularizer, due to its tendency to blur edges, but regularizers which are more edge- and detail-preserving such as the \(L_1\) and Total Variation either risk inducing rotational biases, or are more difficult to obtain convergence and interpret L-curves for. Thus, while the Laplacian is not necessarily the best regularizer in practice, it is a good case study for learning the basics of regularization.